Berikut ini contoh laporan dari kasus inflasi.
BAB I
PENDAHULUAN
1.1 Deskripsi Kasus
Adapun kasus yang akan dibahas pada laporan ini yaitu sebagai berikut.
Kasus : 8
Deskripsi : Berdasarkan data BPS pada tahun 2009 diketahui bahwa inflasi rata-rata di Indonesia adalah 0,23/bulan. Jika data inflasi tersebut diasumsikan berdistribusi eksponensial. Buatlah aplikasi yang mensimulasikan. Lalu berdasarkan hasil simulasi tersebut, carilah rata-rata inflasi per bulan, simpangan baku, dan inflasi terbesar?
1.2 Metode yang digunakan
Berdasarkan deskripsi kasus di atas, maka metode yang akan diambil dalam penyelesaian kasus tersebut yaitu dengan metode distribusi eksponensial.
1.3 Ruang Lingkup dan Asumsi
Untuk mendapatkan nilai acak menggunakan metode LCG (Linear Congruental Generator). Adapun rumus yang digunakan :
Z[i] = ( a . Z[i-1] + c ) mod m
Dimana :
Z[i] = bilangan acak ke-I dari deretnya
Z[i-1] = bilangan acak sebelumnya
a = faktor pengali
c = increment (angka konstan yang bersyarat)
m = modulus (modulo)
kunci pembangkit Z[0] yang disebut seed
Varians yaitu rata-rata perbedaan antara mean dengan nilai masing-masing observasi.
Rumus :
Simpangan baku yaitu suatu nilai yang menunjukan tingkat variasi suatu kelompok data .
Rumus : S = √V = √S2
Adapun aplikasi yang digunakan untuk membangun program simulasi ini yaitu menggunakan Borland Delphi 7
BAB II
LANDASAN TEORI
2.1 Distribusi Eksponensial
Fungsi eksponensial adalah salah satu fungsi yang paling penting dalam matematika. Biasanya, fungsi ini ditulis dengan notasi exp(x) atau ex, di mana e adalah basis logaritma natural yang kira-kira sama dengan 2.71828183.
Fungsi eksponensial (merah) terlihat hampir mendatar horizontal (naik secara sangat perlahan) untuk nilai x yang negatif, dan naik secara cepat untuk nilai x yang positif. Sebagai fungsi variabel bilangan real x, grafik ex selalu positif (berada di atas sumbu x) dan nilainya bertambah (dilihat dari kiri ke kanan). Grafiknya tidak menyentuh sumbu x, namun mendekati sumbu tersebut secara asimptotik. Invers dari fungsi ini, logaritma natural, atau ln(x), didefinisikan untuk nilai x yang positif.
2.1.1 Distribusi Eksponensial Bivariat
Distribusi Eksponensial pertama kali diperkenalkan oleh Gupta dan Kundu pada tahun 1999. Distribusi ini diambil dari salah satu fungsi kepadatan kumulatif yang digunakan pada pertengahan abad 19 (Gompertz-Verhulst) untuk membandingkan tabel kematian dan menghasilkan laju pertumbuhan penduduk, yang didefinisikan sebagai berikut:
Keterangan:
x = peubah acak
 = parameter bentuk
= parameter bentuk
e = 2,7183...
Untuk α > 0 dan λ > 0 masing–masing adalah parameter bentuk dan parameter skala. Ini jelas untuk α = 1, merupakan distribusi eksponensial. Pada kajian parameter α, dan λ = 1, sehingga distribusi eksponensial tergeneralisir dengan parameter bentuk di notasikan dengan GE(α).
Jika terdapat dua peubah acak (X1,X2) yang berdistribusi eksponensial tergeneralisir dengan asumsi saling bebas, maka distribusi eksponensial tergeneralisir dua variabel (fungsi kepadatan peluang gabungan dari (X1,X2)), untuk x1 > 0, x2 > 0 adalah:
2.2 Pengertian Delphi
Delphi adalah kompiler / penterjemah bahasa Delphi (awalnya dari Pascal) yang merupakan bahasa tingkat tinggi sekelas dengan Basic atau C yang merupakan produk dari Borland corp. Bahasa Pemrograman di Delphi disebut bahasa procedural artinya bahasa/sintaknya mengikuti urutan tertentu / prosedur. Delphi termasuk Keluarga Visual sekelas Visual Basic, Visual C, artinya perintah-perintah untuk membuat objek dapat dilakukan secara visual. Pemrogram tinggal memilih objek apa yang ingin dimasukkan kedalam Form/Window, lalu tingkah laku objek tersebut saat menerima event/aksi tinggal dibuat programnya.
Ada jenis pemrograman non-prosedural seperti pemrograman untuk kecerdasan buatan seperti bahasa Prolog. Delphi merupakan bahasa berorentasi objek, artinya nama objek, properti dan methode/procedure dikemas menjadi satu kemasan (encapsulate).
Sebelum mempelajari ketiga struktur pemrograman ada baiknya kenali dahulu tampilan IDE, yang merupakan editor dan tools untuk membuat program Delphi. Pada IDE akan ditampilkan Form baru yang merupakan aplikasi/program Window yang akan dibuat.Aplikasi / program berbasis windows sering disebut dengan jendela (window).
Sebelum mempelajari ketiga struktur pemrograman ada baiknya kenali dahulu tampilan IDE, yang merupakan editor dan tools untuk membuat program Delphi. Pada IDE akan ditampilkan Form baru yang merupakan aplikasi/program Window yang akan dibuat.Aplikasi / program berbasis windows sering disebut dengan jendela (window).
Bagaimana membuat aplikasi berbasis windows (berbasis grafik dan bukan berbasis teks seperti pada DOS)? Caranya dengan membuat sebuah form. Pada pemrograman berbasis windows, kita akan diperhadapkan pada satu atau beberapa jendela yang nampak dihadapan kita. Jendela ini dalam Delphi disebut juga dengan form.
Pada pemrograman berbasis windows, kita akan diperhadapkan pada satu atau beberapa jendela yang nampak dihadapan kita. Jendela ini dalam Delphi disebut juga dengan form.Delphi adalah sebuah perangkat lunak (bahasa pemrograman) untuk membuat program / aplikasi komputer berbasis windows. Delphi merupakan bahasa pemograman berbasis objek, artinya semua komponen yang ada merupakan objek-objek.
Ciri sebuah objek adalah memiliki nama, properti dan method/procedure. Delphi disebut juga visual programming artinya komponen-komponen yang ada tidak hanya berupa teks (yang sebenarnya program kecil) tetapi muncul berupa gambar-gambar.
Instalasi Delphi 7 pada lingkungan windows, seperti instalasi pada program-program aplikasi di lain di windows. Untuk lingkungan Linux, Borland menyediakan Borland Kylix yang merupakan versi Linux dari Borland Delphi.
Pada pemrograman berbasis windows, kita akan diperhadapkan pada satu atau beberapa jendela yang nampak dihadapan kita. Jendela ini dalam Delphi disebut juga dengan form.Delphi adalah sebuah perangkat lunak (bahasa pemrograman) untuk membuat program / aplikasi komputer berbasis windows. Delphi merupakan bahasa pemograman berbasis objek, artinya semua komponen yang ada merupakan objek-objek.
Ciri sebuah objek adalah memiliki nama, properti dan method/procedure. Delphi disebut juga visual programming artinya komponen-komponen yang ada tidak hanya berupa teks (yang sebenarnya program kecil) tetapi muncul berupa gambar-gambar.
Instalasi Delphi 7 pada lingkungan windows, seperti instalasi pada program-program aplikasi di lain di windows. Untuk lingkungan Linux, Borland menyediakan Borland Kylix yang merupakan versi Linux dari Borland Delphi.
BAB III
PENYELESAIAN SIMULASI
3.1 Flowchart Proses Simulasi
Flowchart difungsikan sebagai gambaran proses program yang telah dibuat. Adapun flowchart dari program simulasi ini adalah sbagai berikut.
3.2 Proses Perhitungan Variabel Simulasi
Adapun proses perhitungan dari variable simulai yaitu :
1. Tampilan awal proses simulasi inflasi adalah sebagai berikut :
2. Penyelesaian kasus
Diketahui data BPS pada tahun 2009 tingkat inflasi rata-rata adalah 0.23/bulan.
Ditanyakan rata-rata inflasi/bulan simpangan baku dan inflasi terbesar, jika akan di simulasikan selama 24 bulan dan data inflasi di asumsikan berdistribusi eksponensial.
Rata-rata inflasi ( β ) = 0.23/bulan
Waktu simulasi = 24 bulan
Nilai awal Z[0] = 123456
Dari data di atas diketahui
Rata-rata inflasi perbulan : 0.171196885682896
Simpangan Baku : 0.20919477577552
Inflasi Terbesar : 0.20919477577552
Tabel hasil simulasi
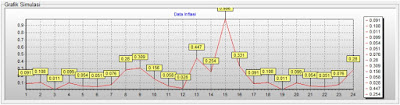
Grafik hasil simulasi
---- Semoga Bermanfaat ----








No comments:
Post a Comment
Silakan masukkan komentar Anda untuk perkembangan blog ini.